Advanced Deterministic Iterative Steady-State Solver
Advanced deterministic iterative steady-state solver
The advanced deterministic iterative steady-state solver (adiss)[1] solves for instant-of-time variables with 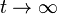 , using a two-stage iterative method that takes advantage of the structure of the probability transition matrix of an embedded Markov chain. Normally, for a large Markov chain, the whole probability transition matrix,
, using a two-stage iterative method that takes advantage of the structure of the probability transition matrix of an embedded Markov chain. Normally, for a large Markov chain, the whole probability transition matrix, 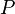 , cannot be stored in core memory and it must be stored on disk. However, that drastically increases the computation time. adiss exploits the structure of
, cannot be stored in core memory and it must be stored on disk. However, that drastically increases the computation time. adiss exploits the structure of 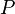 by using a “decomposability factor,”
by using a “decomposability factor,”  , to decompose it into two matrices,
, to decompose it into two matrices, 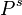 and
and 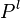 , such that
, such that 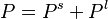 and all elements of
and all elements of 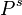 are less than
are less than  . For large models,
. For large models, 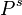 can be stored on disk, while
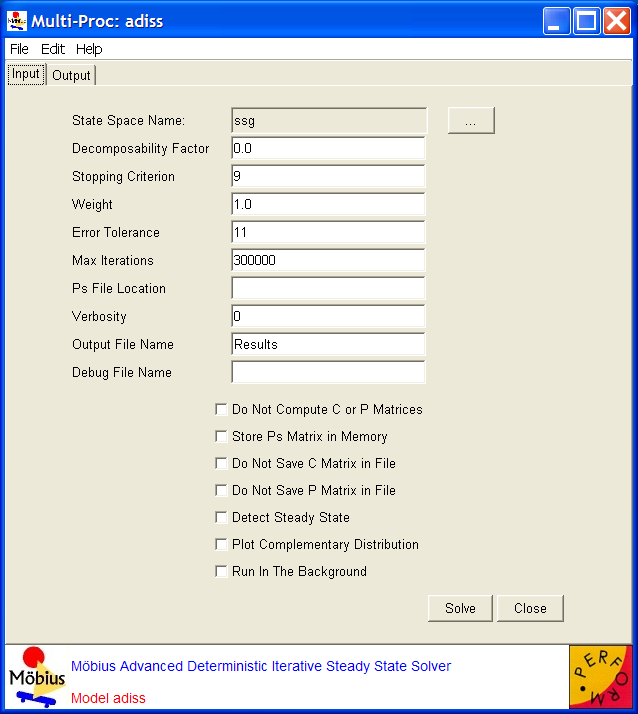
can be stored on disk, while 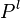 can be stored in core memory so that it can be accessed more often in the iterative process. Solution is restricted to models in which there is no more than one deterministic action enabled in each process state. adiss calculates the mean and variance of each performability variable. The means and variances are given in textual format in an output file. <xr id="fig:adissSolver" /> shows the editor for the advanced deterministic iterative steady-state solver and its available options and adjustable parameters.
can be stored in core memory so that it can be accessed more often in the iterative process. Solution is restricted to models in which there is no more than one deterministic action enabled in each process state. adiss calculates the mean and variance of each performability variable. The means and variances are given in textual format in an output file. <xr id="fig:adissSolver" /> shows the editor for the advanced deterministic iterative steady-state solver and its available options and adjustable parameters.
<figure id="fig:adissSolver">
The options are as follows:
- The Decomposability Factor is a double-precision float representing the threshold for decomposing the probability transition matrix
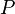 .
.
- The Decomposability Factor is a double-precision float representing the threshold for decomposing the probability transition matrix
- The Weight is a double precision float representing the acceleration factor. 1.0 is the default. A value of 1.0 reduces the SOR method to Gauss-Seidel. Values between 1.0 and 2.0 may accelerate convergence. Values between 0.0 and 1.0 are less subject to divergence.
- The Error Tolerance is a short integer representing a negative power of 10 (i.e., error tolerance) for truncation of infinite series during calculation of the Poisson probabilities. 11 is the default value. Increasing the error tolerance may increase the solution time. The solution time can be reduced if more error can be tolerated.
- The Max Iterations is an unsigned long representing the maximum number of iterations that will be performed before the solver terminates. 300,000 is the default.
- The Ps File Location is the path to the file containing the previously stored matrix
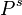 .
.
- The Ps File Location is the path to the file containing the previously stored matrix
- The Verbosity (
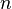 ) sets a trace level of intermediate output. The default is no intermediate output. If
) sets a trace level of intermediate output. The default is no intermediate output. If 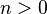 , then the accuracy is printed after every
, then the accuracy is printed after every 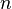 iterations.
iterations.
- The Verbosity (
- If Do Not Compute C or P Matrices is selected, the
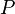 and
and 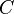 will not be computed explicitly.
will not be computed explicitly.
- If Do Not Compute C or P Matrices is selected, the
- If Store Ps Matrix in Memory is selected, the solver stores the matrix
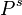 in memory to help speed up the solution process. If the solver complains of insufficient memory, this option should be selected so that the matrix is stored in a file.
in memory to help speed up the solution process. If the solver complains of insufficient memory, this option should be selected so that the matrix is stored in a file.
- If Store Ps Matrix in Memory is selected, the solver stores the matrix
- If Do Not Save C Matrix in File is not selected, the solver saves rows of the
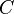 matrix in a file instead of keeping them in memory. Saved rows are read back at appropriate times. This option should be used when there is enough main memory to store the matrix. Storing the matrix in memory will help to speed up the solution process.
matrix in a file instead of keeping them in memory. Saved rows are read back at appropriate times. This option should be used when there is enough main memory to store the matrix. Storing the matrix in memory will help to speed up the solution process.
- If Do Not Save C Matrix in File is not selected, the solver saves rows of the
- If Do Not Save P Matrix in File is not selected, the solver saves rows of the
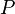 matrix in a file instead of keeping them in memory. Saved rows are read back at appropriate times. This option should be used when there is enough main memory to store the matrix. Storing the matrix in memory will help to speed up the solution process.
matrix in a file instead of keeping them in memory. Saved rows are read back at appropriate times. This option should be used when there is enough main memory to store the matrix. Storing the matrix in memory will help to speed up the solution process.
- If Do Not Save P Matrix in File is not selected, the solver saves rows of the
- If Detect Steady State is selected, the solver detects the steady state. It can reduce the solution time, but you should compare the results obtained with and without this option to make sure that steady-state is not falsely detected.
The output file contains the means and variances of the performability variables. It also contains the following information:
- The index of deterministic action considered, which is an index into an internal data structure of the deterministic action that is being processed. The number itself is not useful, only the fact that progress is being made.
- The left truncation point, which is the number of iterations below which uniformization does not collect results.
- The right truncation point, which is the number of iterations above which uniformization does not collect results.
- The number of iterations required for convergence.
- The maximum difference, which is the maximum difference between the cells in the
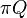 and zero vectors, which represents the error. The truncation error is not reported, but is bounded by the specified error tolerance.
and zero vectors, which represents the error. The truncation error is not reported, but is bounded by the specified error tolerance.
- The maximum difference, which is the maximum difference between the cells in the
Pitfalls and Hints
- The adiss solver suffers from the fill-in problem, albeit to a lesser extent than the dss solver. For every marking in which a deterministic action is enabled, the transition probabilities to all the markings that can be reached during the deterministic time are computed. Depending on the model, this results in a considerable number of fill-ins if a high percentage of the markings enable deterministic actions. One example that leads to many fill-ins is a single buffer with a deterministic server; the deterministic action is enabled in all markings that represent at least one job in the buffer. Consequently, considerable fill-ins will occur.
- The instant-of-time steady-state measure is not necessarily defined for models with deterministic actions, because periodic behavior may exist. The outcome of adiss can in that case be interpreted as the time-averaged interval-of-time steady-state measure. However, that interpretation is valid when only rate rewards are considered (i.e., no measures with impulse reward are defined). Furthermore, the variance and distribution that are derived do not have any meaning for the interval-of-time variables.
- adiss cannot solve models having deterministic actions with delay values that are marking-dependent. If the specified model contains a marking-dependent deterministic action, the obtained results should be discarded.
- For decomposability factors equal to zero, the solution method of this solver is the same as that of the power method.
References
- ↑ L. Malhis and W. H. Sanders. An Efficient Two-Stage Iterative Method for the Steady-State Analysis of Markov Regenerative Stochastic Petri Net Models. Performance Evaluation, 27&28:583–601, 1996.