Iterative Steady-State Solver
Iterative steady-state solver
The iterative steady-state solver (iss) solves for instant-of-time variables with 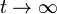 . Two iterative methods are provided in Möbius for this solver: successive over-relaxation (SOR) and Jacobi. iss solves the system of equations given by
. Two iterative methods are provided in Möbius for this solver: successive over-relaxation (SOR) and Jacobi. iss solves the system of equations given by 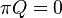 , where
, where 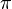 is the state occupancy probability vector and
is the state occupancy probability vector and 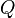 is the generator matrix. The algorithm guesses
is the generator matrix. The algorithm guesses 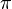 , calculates
, calculates 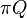 , and then comes up with a new guess related to the difference between the answer and the zero vector. It continues until the maximum difference between the cells in the two vectors is within the error bounds.
, and then comes up with a new guess related to the difference between the answer and the zero vector. It continues until the maximum difference between the cells in the two vectors is within the error bounds.
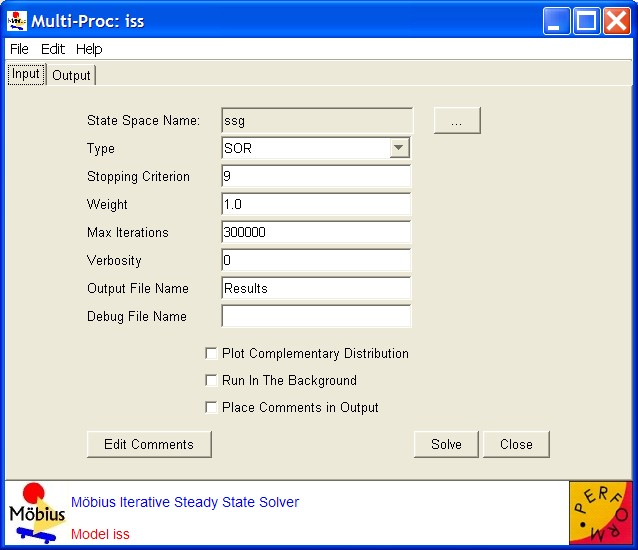
The initial guess for 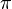 is equal probabilities for all states. The acceleration factor to be used must be selected by the user. Because of its more modest space requirements, this solver can be applied to larger models than dss can, but it is not guaranteed to converge for all state spaces and initial conditions. It calculates the mean and variance for each performability variable. The means and variances are recorded in textual format in an output file. <xr id="fig:issSolver" /> shows the editor for the iterative steady-state solver and its available options and adjustable parameters.
is equal probabilities for all states. The acceleration factor to be used must be selected by the user. Because of its more modest space requirements, this solver can be applied to larger models than dss can, but it is not guaranteed to converge for all state spaces and initial conditions. It calculates the mean and variance for each performability variable. The means and variances are recorded in textual format in an output file. <xr id="fig:issSolver" /> shows the editor for the iterative steady-state solver and its available options and adjustable parameters.
<figure id="fig:issSolver">
The options are as follows:
- The Type of iterative method refers to either SOR or Jacobi. In general, SOR should be used because it converges in fewer iterations and it has smaller memory requirements than Jacobi. However, because SOR requires that the underlying generator matrix be accessible in column order, it cannot be used with state spaces generated by the symbolic state-space generator (see Section 2.3 for more details). Use Jacobi instead for these state spaces because accesses to the matrix elements are not provided in any particular order.
- The Weight is a double representing the acceleration factor. 1.0 is the default. A value of 1.0 reduces the SOR method to Gauss-Seidel. Values between 1.0 and 2.0 may accelerate convergence. Values between 0.0 and 1.0 are less subject to divergence.
- The Max Iterations is an integer representing the maximum number of iterations that will be performed before the solver terminates. 300,000 is the default.
- The Verbosity (
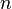 ) sets the trace level of intermediate output. The default is no intermediate output. If
) sets the trace level of intermediate output. The default is no intermediate output. If 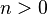 , then the accuracy is printed after every
, then the accuracy is printed after every 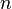 iterations.
iterations.
- The Verbosity (
The output file contains the mean and variance of the performability variables. It also contains the following information:
- the number of iterations required for convergence,
- the maximum difference, which is the maximum difference (over all the states) between the solution in the last two iterations.
Pitfalls and Hints
- The iss solver can be used for many practical models. A required condition for these models is that they are ergodic Markovian models. Otherwise, if the model contains one or more absorbing states, iss cannot be used; it will produce the message iss_solver: zero on the diagonal and quit. To find out whether the model has absorbing states, apply the Flag Absorbing States option in the state space generator.
- The iss algorithm stops when the largest difference of the state probabilities between two iterations (at that moment not yet normalized to sum to 1) is less than the specified error. This stopping criterion does not directly relate to the error between the derived and the real state probabilities, let alone between the derived and the real performability variables. A value of 10-9 for the Accuracy will usually be sufficient.
- As a rule of thumb, the additional time it takes to get
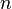 times as accurate a result is of the order
times as accurate a result is of the order 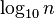 . Hence, increasing accuracy tends to be not too costly. Of course, the machine accuracy can never be exceeded.
. Hence, increasing accuracy tends to be not too costly. Of course, the machine accuracy can never be exceeded.
- As a rule of thumb, the additional time it takes to get
- First try iss with Weight equal to 1. This usually leads to quick solutions. A higher weight may decrease the number of iterations; however, an (even slightly) too high weight can dramatically increase the necessary number of iterations. If iss does not converge for a Weight of 1.0, try values lower than 1.0. Typically, making Weight
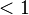 improves convergence, while Weight
improves convergence, while Weight 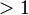 decreases the number of iterations if convergence has already been assured. Note that the value of Weight should be between 0 and 2.
decreases the number of iterations if convergence has already been assured. Note that the value of Weight should be between 0 and 2.
- First try iss with Weight equal to 1. This usually leads to quick solutions. A higher weight may decrease the number of iterations; however, an (even slightly) too high weight can dramatically increase the necessary number of iterations. If iss does not converge for a Weight of 1.0, try values lower than 1.0. Typically, making Weight
- The iss solver usually derives results in a reasonable amount of time. If the state space is large, more computation is necessary per iteration, but the number of iterations is often relatively low. Therefore, initially use the default for the number of iterations. If iss does not converge within a reasonable number of iterations, you may have set the accuracy too high for the machine being used. Be careful in choosing an accuracy smaller than 10-10 (i.e., an input value of 10 for Accuracy). You can check the progress toward convergence of iss by using the Verbosity option.
- Some models may require many iterations. They are called stiff models and belong to the class of nearly-decomposable models. They occur, for example, when the performance of a system quickly reaches some state that initially seems to be a steady state for any system configuration; however, the actual steady state is a different state and changes from the initial state take place very slowly and infrequently. This is due to the large difference in the rates of the actions in the individual models.