PEPA Atomic Formalism
PEPA
Möbius supports PEPA as an atomic modeling formalism. PEPA is a process algebra. Instead of creating a PEPA atomic model in a graphical editor, the model is created using an editor provided in Möbius in a form that resembles a formal language. Möbius extends the basic PEPA language to include process parameters, guards, and value passing. This extension is known as the PEPAk language.
The PEPAk language
This section covers the basic building blocks of the PEPAk language including process variables, formal parameters, guards, choices, prefixes, hide, and cooperation.
- Process Variable: In the PEPAk language, processes are represented using process variables. A process variable is defined by assigning an equation to a symbolic name using the assignment operator “
 ”. For example, the following defines the process variable
”. For example, the following defines the process variable 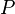 :
:
- Process Variable: In the PEPAk language, processes are represented using process variables. A process variable is defined by assigning an equation to a symbolic name using the assignment operator “
![P[a]](/wiki/images/math/6/d/c/6dc5c5fa6d4db7db59dce76d5f892bdf.png)
|

|
|
![[a > 5] => (\alpha,x).P[a-1]](/wiki/images/math/8/6/f/86f9f6da65296e4c09369d62c6adf194.png)
| ||
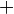
|
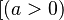 && && ![(a < 5)] => (\beta,x).P[a-1];](/wiki/images/math/8/5/8/858c8df4a4a0ca9ffddefddf6d20ef02.png)
|
- Formal Parameters: The PEPAk language extends PEPA to include the possibility of formal parameters for process variables. In the example above the process variable
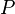 takes a single parameter,
takes a single parameter, 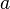 . More parameters may be specified by a comma delimited list as follows:
. More parameters may be specified by a comma delimited list as follows: ![P[a,b]](/wiki/images/math/6/9/a/69a87766898eaff9fdde5cee2ecc899c.png) .
.
- Formal Parameters: The PEPAk language extends PEPA to include the possibility of formal parameters for process variables. In the example above the process variable
- Guards: The introduction of guards to the PEPAk language allows the selective enabling and disabling of a process expression based on the guard conditions. A process expression is enabled if its guard evaluates to true, and disabled if its guard evaluates to false. Guards are represented by boolean expressions enclosed in square brackets before a process expression, and may contain references to formal parameters. In the above example, the two process expressions are guarded by conditions,
![[a > 5]](/wiki/images/math/3/a/8/3a8bb12c62a2ca4822d31f2f9c1104b2.png) , and
, and 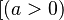 &&
&& ![(a < 5)]](/wiki/images/math/f/e/5/fe5ae60b27264317057ad1cbec87f551.png) . Thus the first process expression is enabled only if the parameter
. Thus the first process expression is enabled only if the parameter 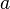 is greater than five, and the second process expression is enabled only if the parameter
is greater than five, and the second process expression is enabled only if the parameter 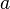 is greater than zero and less than five. The guard operator “
is greater than zero and less than five. The guard operator “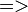 ” assigns a process expression to a given guard expression.
” assigns a process expression to a given guard expression.
- Guards: The introduction of guards to the PEPAk language allows the selective enabling and disabling of a process expression based on the guard conditions. A process expression is enabled if its guard evaluates to true, and disabled if its guard evaluates to false. Guards are represented by boolean expressions enclosed in square brackets before a process expression, and may contain references to formal parameters. In the above example, the two process expressions are guarded by conditions,
- Choice: The choice operator “
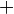 ” is used to allow a process to behave in different ways under different circumstances as defined by a process expression. The first enabled process expression to complete is selected and the remainder of the expressions are discarded. In the above example we see a choice between two guarded process expressions.
” is used to allow a process to behave in different ways under different circumstances as defined by a process expression. The first enabled process expression to complete is selected and the remainder of the expressions are discarded. In the above example we see a choice between two guarded process expressions.
- Choice: The choice operator “
- Prefix: The simplest way to describe the behavior of a process is to add a prefix to the preferences to the process variable. Prefixes are denoted using the form
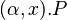 , where
, where 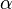 is some action which has a duration that is exponentially distributed with rate
is some action which has a duration that is exponentially distributed with rate 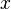 . After the action has completed, it then behaves according to the referenced process variable. In the case of a choice between multiple enabled processes expressions, it is the activity that completes first which is selected.
. After the action has completed, it then behaves according to the referenced process variable. In the case of a choice between multiple enabled processes expressions, it is the activity that completes first which is selected.
- Prefix: The simplest way to describe the behavior of a process is to add a prefix to the preferences to the process variable. Prefixes are denoted using the form
- Hide: The hide operator “
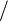 ” is a combinator that is used to hide activities. With respect to a process, the hidden activities are considered silent. As in many other process algebras, the combinator is used to express abstraction.
” is a combinator that is used to hide activities. With respect to a process, the hidden activities are considered silent. As in many other process algebras, the combinator is used to express abstraction.
- Hide: The hide operator “
- Cooperation: Processes
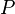 and
and 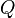 are said to cooperate over a set of shared activities if they contain one or more shared activities and are defined as cooperating over these activities. They are defined as cooperating over an activity through the definition of a new process variable as follows:
are said to cooperate over a set of shared activities if they contain one or more shared activities and are defined as cooperating over these activities. They are defined as cooperating over an activity through the definition of a new process variable as follows:
- Cooperation: Processes
![S = P[x] <\alpha> Q[y]](/wiki/images/math/3/f/0/3f0554e65d4d5640596af1fd5ce8e5fc.png)
- The “
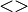 ” operator is the cooperation operator and takes its parameters as a comma delimited list of activities to be shared between the cooperating processes. If a process enables an activity within the shared set, it will not be able to continue with the activity until the cooperating process also enables this activity. Both processes then complete the shared activity. When defining a prefix for a shared activity, one of the cooperating processes may define it with rate
” operator is the cooperation operator and takes its parameters as a comma delimited list of activities to be shared between the cooperating processes. If a process enables an activity within the shared set, it will not be able to continue with the activity until the cooperating process also enables this activity. Both processes then complete the shared activity. When defining a prefix for a shared activity, one of the cooperating processes may define it with rate 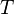 , indicating that it is a passive activity and the duration of the activity is to be determined based on the duration generated by the other cooperating process, illustrated in the following example:
, indicating that it is a passive activity and the duration of the activity is to be determined based on the duration generated by the other cooperating process, illustrated in the following example:
- The “
![C[a,b]](/wiki/images/math/d/9/3/d930e3053f32dbc51f14e870df59674d.png)
|

|
![[a > 0] \rightarrow (o_1, r_1).C[a-1,b]](/wiki/images/math/1/6/c/16c490521d054229cab4c4e6b610df2d.png)
|
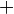
|
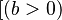 && && ![(a == 0)] => (o_2, r_2).C[a,b-1];](/wiki/images/math/7/4/e/74e0298e13626a54601f7e9f71602a82.png)
| |
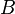
|

|
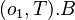
|
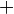
|
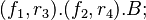
| |
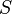
|

|
![C[0,0] <o_1> B;](/wiki/images/math/6/f/8/6f83a82641c255a33695e5ad19f8d39e.png)
|
Note that, in order to solve a PEPAk model using any of the Möbius solvers (see Solving Models), the underlying Markov chain must have a finite state space and must be irreducible and ergodic. A necessary (although not sufficient) condition for this is that the model is composed from the processes using the hide or cooperation combinator. These combinators are static in the sense that they are not “destroyed” by activity transitions. The necessary condition ensures that the structure of the model does not grow unboundedly over time.